Virtual World Structure
A UNIGINE-based virtual world is a scene that contains a set of different built-in objects with certain properties assigned to them. Almost all objects are visible in the virtual world. However, some of them are pseudo-objects, which cannot be seen in a normal mode (such as physicals, occluders, and so on).
In general, a world includes:
- Built-in objects called nodes, which may refer to other nodes (*.node), meshes (*.mesh), audio files (*.oga), paths (*.path), or scripts (*.h)NoticeA world can store both nodes themselves and/or references to nodes stored in external *.node files. A *.node file can also store both nodes and references to other external *.node files.
- Materials and properties
- Shaders and textures to which materials refer
- General rendering, physics, sound and game settings
A new world can be created via the Menu bar of UnigineEditor or via UNIGINE SDK Browser when creating a new project.
Each world is stored on the disk in a separate file in the XML format with the .world extension. The world content is generated and managed via UnigineEditor.
You can also generate and manage content via world logic: UnigineScript file (*.usc) for projects that use UnigineScript only, AppWorldLogic.cpp for C++ applications, or AppWorldLogic.cs for C# applications.
Worlds can be as large as a level designer wishes, because UNIGINE supports data streaming, and required resources — meshes, textures, animations, sounds — are dynamically loaded at run time. Resources that are no longer needed are unloaded from memory.
For common outdoor scenes, we recommend you to use the scale 1 unit = 1 meter, when you export objects from 3D modeling software.
To make the large-world designing and editing process easier, you can split your world into several parts.
Coordinate System#
UNIGINE uses the right-handed Cartesian coordinate system: X and Y axes form a horizontal plane, Z axis points up. When exporting animation from 3D editors, Y is considered a forward direction.

Positive rotation angle sets rotation counterclockwise. The right-hand rule applies: if you set the right hand thumb along the axis, other fingers wrapped will show the rotation direction.

Built-in Objects#
UNIGINE provides a set of built-in objects that allow adding to a world practically all objects existing in real life. For convenience, they are divided into several groups according to the type of operation.
A world can store both nodes themselves and/or references to nodes stored in external files with the .node extension.
Nodes of object-related types may have surfaces and physical bodies (including collision shapes connected using joints). Surfaces contain references to particular materials and properties. Such references are created automatically when you assign a material or a property to a surface.
A surface serves as an atomic rendering unit and can represent:
- A part of the object that has its own separate material.
- Different levels of details (LODs) (including reflection LODs and shadow LODs). In this case surfaces represent the same object or its part in a more and a less detailed variants (a high-polygonal and a low-polygonal model). Which of these surfaces is visible is determined by the surface properties.
Each surface can also have several morph targets (blend shapes).
Taking into account the information given above, the scheme of the world components can be extended as follows:
Nodes Hierarchy#
All nodes are organized into a hierarchy. Each node can have multiple children.

Usually coordinates and orientation of the first-level nodes are set in the global (world) coordinate system, while coordinates and orientation of their child nodes are in local coordinate systems of their parents (if not chosen otherwise). So you can transform and rotate the whole hierarchy tree branch only by transforming and rotating its root node.
The origin of the global (world) coordinate system is located at the scene center. The origin of the local coordinate system is at the pivot point of the parent node.
Surfaces#
As mentioned above, nodes of object-related types can have surfaces. By default, such a node added via UnigineEditor has one surface.
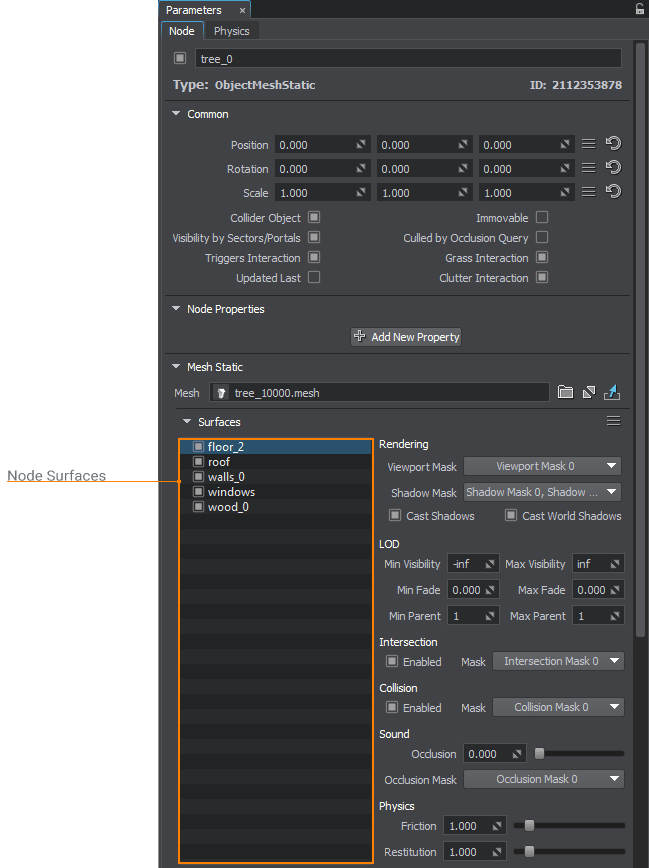
The number of surfaces depends on how a mesh was imported into UNIGINE and cannot be changed dynamically at run time. However, you can reimport it via UnigineEditor, if necessary. Each surface may add a separate DIP call to the GPU.
Surfaces also participate in culling of invisible parts of the object when the object is hidden behind other objects. Moreover, surfaces are used to calculate collision detection with physically simulated objects.
Nodes share common options for their surfaces. Each surface can be enabled or disabled for rendering, as needed. Surfaces cannot be added, deleted, or otherwise altered in UnigineEditor. The reason is that surfaces are formed during the object creation in an external 3D editor. To change them, you should re-import the object.
You can assign a separate material and property to each surface.
Surfaces often represent LODs of the same object. For more details about Min parent, Max parent, Visibility and Fade distance parameters, see Levels of details.
Physical Simulation of Objects#
Objects can either be just non-interactive environment or take part in physical simulation. The built-in engine physics is a very rough approximation of the real world that is designed to be effective and at the same time keep the overall framerate high. Its main aim is to detect collisions between the objects.
To participate in collisions, an object should have a body that describes how it can behave and what physical properties it possesses. For example, an object with a rigid body always stays solid and undeformed, and an object with a cloth body can be folded and torn.
However, the body is not enough for an object to start interacting. Its volume should be approximated using some kind of a physical primitive (or a set of them) — a shape. UNIGINE provides several types of such primitives: box, sphere, capsule, cylinder, convex hull, or an arbitrary mesh shape. The shape is used to compute collisions between objects.
Two shapes can be connected with one of the joints: fixed, ball, hinge, prismatic, cylindrical, wheel or suspension. Joints define how two shapes can move relative to each other.
Materials#
Nodes without materials are rendered red in the scene. The material stores information on how a node is to be rendered; it is in fact a set of properties (states, options, parameters) and assets (2D, 3D textures), based on which surfaces are rendered. The material should be assigned to the node surface.
 |
 |
Material ball with no material assigned |
Material ball with the mesh_base material assigned |
Even if no material is assigned to the node surfaces, the node can still participate in collisions and intersections.
To manage rendering of surfaces with no materials assigned, use the viewport mask for these surfaces.
In UNIGINE, there are two types of materials:
- Read-only base materials created by programmers and stored in *.basemat files. A UNIGINE-based project includes a set of default base materials.
- Editable user materials inherited from the base materials or from other user materials and stored in *.mat files. Such materials are created by 3D artists and override properties of parent materials.
A set of base material properties may include:
- Options. The set of options is pre-defined and invariable for all materials. Each option either enables or disables some kind of behavior. Option values for base materials are hard-coded.
- States. Conditions based on which UNIGINE selects appropriate shaders, textures, and parameters. For example, one can define a state that turns on and off rendering of foam in water simulation and provide different shaders for both states (with and without foam).
- Textures. Usually, the base material has several textures defined. The common reasons for that are the following:
- A shader may need more than one texture for processing.
- Different textures can be used in different rendering passes.
- States may influence the number of textures, for example, each state may require its own texture.
- Parameters. The values passed as arguments to relevant shaders.
- Shaders. The programs that actually draw the material based on different conditions.
NoticeEach base material is usually equipped with several shaders, and the appropriate one is chosen according to the current rendering pass and state.Only base materials can refer to shaders.
A set of user material properties cannot differ from the base material ones: the user material inherited from the base material only overrides all its options, states, textures and parameters.
UNIGINE allows creating manual materials. These materials are created and edited manually: changes made via UnigineEditor at run time won't be saved. All base materials (both built-in and custom ones) are manual. However, not every manual material is the base one: user materials can be manual, too.
Material Hierarchy#
In UNIGINE, materials are organized into a hierarchy, like nodes, but are completely independent from the node hierarchy.
A parent material passes its properties to the inherited material so that they can be overridden.
Base materials cannot be organized into a hierarchy: no base material can be inherited from another base material. However, if you need to modify properties of a base material, you can create a new user material by inheriting from the required base material: the base material will pass its properties to the inherited material and you can override them. Thus, the base materials are always on the top of the material hierarchy.
Materials hierarchy is based on GUIDs. For base and manual materials, GUIDs are generated at run time by using their names stored in materials files. As for user materials, they are also generated at run time on materials' creation and stored in the *.mat files. However in materials files, references to materials can be name-based or GUID-based.
At cloning or inheriting a material, each new material becomes internal until a name is assigned to it.
The loading order of materials doesn't matter: on the engine start-up, all materials of the project are loaded, base materials are loaded first. And since each *.mat material refers to both the parent and the base materials, the base material is used as the parent one until the parent is loaded. So, when the application is loaded, all materials existing in the project are presented in the materials hierarchy.

 |
 |
Material ball with mesh_base material assigned |
Material ball with a user material inherited from mesh_base |
The left material ball is rendered using one of the built-in base materials. The right material ball inherits its material from that base and simply changes 2 textures (the albedo and normal textures). There is no need to set other properties, as they are inherited. However, if necessary, you may change any property, just like we've changed the texture for the material ball.
All material properties (except shaders) can be easily overridden in UnigineEditor. However, if you need to extend a set of existing properties or override shaders, you need to create a custom material. In this case also check the Materials Files section for a detailed description of material declarations in XML.
Properties#
Just defining the object's position, inherent characteristics, and outside appearance is not enough to integrate the object into the world correctly. Properties specify the way the object will behave and interact with other objects and the scene environment.
A property is a "material" for application logic represented by a set of logic-related parameters. Properties can be used to build components to extend the functionality of nodes.
You can define conditions for parameters of the property to be available/unavailable in UnigineEditor.
UNIGINE's Properties system includes:
- Manual properties implemented and modified manually by programmers. A manual property at the top of the hierarchy is called a base property. There are two built-in read-only base properties: node_base and surface_base.
- User properties inherited from the manual ones and adjusted via the UnigineEditor by 3D artists.
Properties can be assigned to both the whole node and a single surface:
- If assigned to a node, properties can specify additional settings that extend the built-in ones (e.g., they can be used to specify if a node is interactive and whether it is a switch). For a character, properties can be used to specify health points or gold amount.
NoticeYou can assign multiple properties to a single node.
- If assigned to a surface, a property can specify certain parameters that can be used during physical interaction with the surface. For example, the property can indicate the type of material assigned to the surface (wood, metal, plastic, etc.).
NoticeOnly one property can be assigned to a surface.
Thus, properties make nodes follow the game/application logic.
If you need to assign a property to a single surface, it is recommended to inherit it from the surface_base property.
We also recommend inheriting properties that will be assigned to nodes from the node_base property. However, you can also assign any custom base property or its children to a node.
To assign a property, use one of the available ways.
Each property is stored in a separate *.prop file, except for the internal properties.
Property Hierarchy#
Properties in UNIGINE, just like materials, are organized into their own independent hierarchy. This hierarchy is formed by inheriting one property from another. A parent property passes all its parameters to its children so that they can be overridden, much like in the object-oriented programming.

The Properties hierarchy is based on GUIDs: all properties are referred to using GUIDs, even the base and manual ones (the GUIDs for such properties are generated at run time and are uniquely determined by their names). However, only user properties store their GUIDs explicitly: a GUID is generated automatically at the user property creation and is written to the corresponding *.prop file.
Properties in the hierarchy can be reparented, renamed, cloned, inherited, or removed in a single click.
The information on this page is valid for UNIGINE 2.20 SDK.

