Matrix Transformations
A lot of calculations in Unigine are performed by using matrices. Actually, matrix transformations are one of the main concepts of 3D engines. This article contains an explanation of matrix transformations with usage examples.
See Also#
- An article about mat4 and dmat4 Unigine data types.
- The description of Math Matrix Functions.
Transformations#
In simple terms, a matrix in 3D graphics is an array of numbers arranged in rows and columns:

Usually, 4x4 matrices are used. Such size (4x4) of matrices is caused by the translation state in 3D space. When you put a new node into the world, it has a 4x4 world transform matrix that defines the position of the node in the world.
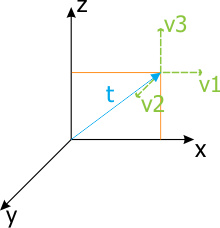
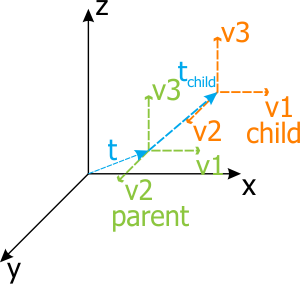
In Unigine, matrices are column major (column-oriented). Hence, the first column of the transform matrix represents the X vector of the local coordinate system (v1), the second represents the Y vector (v2), the third represents the Z vector (v3), and the fourth represent the translation vector t. First three columns show directions of local coordinate axes (rotation) and the scale of the origin. The last column contains the translation of the local origin relatively to the world origin.
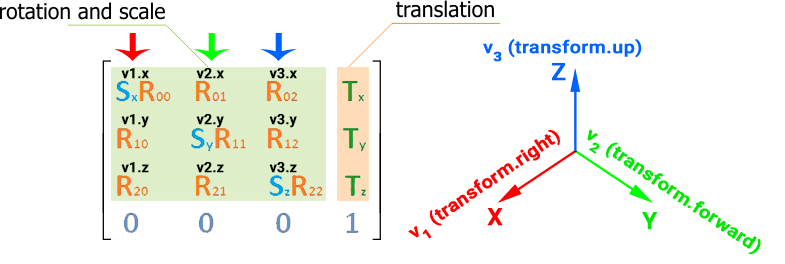
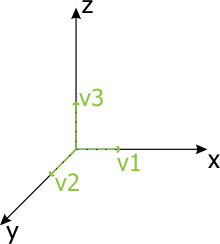
Identity Matrix#
The world origin has the following matrix:

This matrix is called identity matrix, a matrix with ones on the main diagonal, and zeros elsewhere. If a matrix is multiplied by the identity matrix, that won't change anything: the resulting matrix will be the same as it was before multiplying.
If the local origin has the identity matrix, it means the local origin and the world origin are coincident.
Rotation#
To change the orientation of the local origin, the first three columns of the matrix should be changed.
To rotate the origin along different axes, you should use proper matrices:
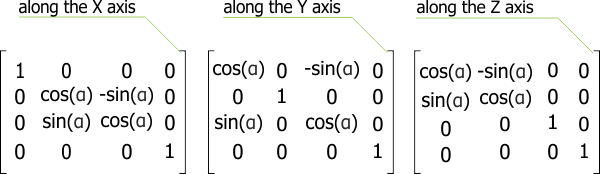
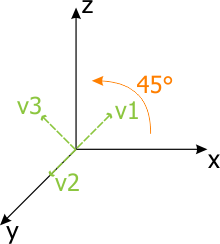
In the matrices given above, α is a rotation angle along the axis.
The next matrix shows the rotation of the local origin along the Y axis at 45 degrees:
|

|
Translation#
The last column of the transform matrix shows the position of the local origin in the world relatively to the world origin. The next matrix shows the translation of the origin. The translation vector t is (3, 0, 2).
|

|
Scaling#
The length of the vector shows the scale coefficient along the axis.
To calculate the vector length (also known as magnitude), you should find a square root of the sum of the squares of vector components. The formula is the following:
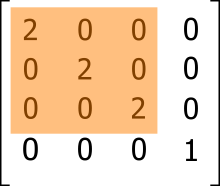
|vector length| = √(x² + y² + z²)The following matrix scales the local origin up to 2 units along all axes.

|
|
Cumulating Transformations#
The order of matrix transformations in code is very important.
If you want to implement a sequence of cumulating transformations, the transformations order in code should be as follows:
TransformedVector = TransformationMatrixN * ... * TransformationMatrix2 * TransformationMatrix1 * VectorTransformations are applied one by one starting from TransformationMatrix1 and ending with TransformationMatrixN.
Example#
This example shows the difference between two orders of matrix transformations.
The code example below adds an ObjectMeshStatic object to the world. In the first case, rotation is followed by translation and in the second case, translation is followed by rotation.
// declare ObjectMeshStatic
ObjectMeshStatic mesh;
/* the init() function of the world script file
*/
int init() {
/* create a camera and add it to the world
*/
Player player = new PlayerSpectator();
player.setDirection(Vec3(0.755f,-1.0f,0.25f));
engine.game.setPlayer(player);
// add the mesh to the editor and set the material
mesh = new ObjectMeshStatic("matrix_project/meshes/statue.mesh");
mesh.setMaterial("mesh_base", "*");
// create the matrix of rotation at 270 degrees angle around Z axis
mat4 rotation = rotateZ(-90);
log.message("rotation matrix is: %s\n", typeinfo(rotation));
// create the translation matrix
mat4 translation = translate(vec3(0,7,0));
log.message("translation matrix is: %s\n", typeinfo(translation));
// cumulate transformations by using the current transformation matrix
mat4 transform = translation * rotation * mesh.getTransform();
mesh.setTransform(transform);
log.message("transformation matrix is:%s\n", typeinfo(mesh.getTransform()));
return 1;
}To change the order, just change the line of cumulating transformations:
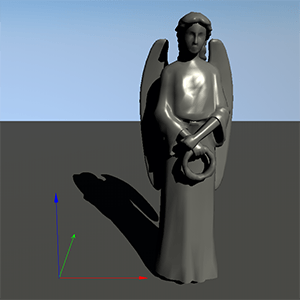
mat4 transform = rotation * translation * mesh.getTransform();The result will be different. The pictures below show the difference (camera is located at the same place).

|
|
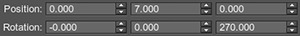
|
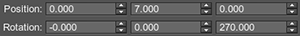
|
|
Order: rotation and translation
|
Order: translation and rotation
|
The pictures above show the position of the meshes related to the world origin.
Matrix Hierarchy#
One more important concept is the matrix hierarchy. When a node is added into the world as a child of another node, it has a transformation matrix that is related to the parent node. That is why the Node class distinguishes between the functions getTransform(), setTransform() and getWorldTransform(), setWorldTransform(), which return the local and the world transformation matrices respectively.
What is the reason of using a matrix hierarchy? To move a node relative to another node. And when you move a parent node, child nodes will also be moved.

|
|
|
Parent origin is the same with the world origin
|
Parent origin has been moved and the child origin has also been moved
|
Pictures above show the main point of the matrix hierarchy. When the parent origin (node) is moved, the chlld origin will also be moved and the local transformation matrix of the child would not be changed. But the world transformation matrix of the child will be changed. If you need the world transformation matrix of the child related to the world origin, you should use the getWorldTransform(), setWorldTransform() functions; in case, when you need the local transformation matrix of the child related to the parent, you should use the getTransform(), setTransform() functions.
Example#
The following example shows the difference between the local and world transformation matrices.
This code is from the UnigineScript world script file. It creates two nodes (child and parent) by using the box.mesh file.
/* declare ObjectMeshStatic objects for nodes
*/
ObjectMeshStatic box_1;
ObjectMeshStatic box_2;
/* the init() function of the world script file
*/
int init() {
/* create a camera and add it to the world
*/
Player player = new PlayerSpectator();
player.setDirection(Vec3(0.755f,-1.0f,0.25f));
engine.game.setPlayer(player);
// add the box mesh to the editor
box_1 = new ObjectMeshStatic("matrix_project/meshes/box.mesh");
// set the transformation and the material for the first box mesh
mat4 transform = translate(vec3(0.0f,0.0f,0.0f));
box_1.setWorldTransform(mat4(transform));
box_1.setMaterial("mesh_base", "*");
// add the second box mesh to the editor
box_2 = new ObjectMeshStatic("matrix_project/meshes/box.mesh");
// set the transformation and the material for the second box mesh
mat4 transform1 = translate(vec3(0.0f,2.0f,1.0f));
box_2.setWorldTransform(Mat4(transform1));
box_2.setMaterial("mesh_base", "*");
// add the second box mesh as a child to the first box mesh
box_1.addChild(box_2);
// show the transformation matrix and the world transformation matrix of the child node
log.message("transformation matrix of the child node: %s\n", typeinfo(box_2.getTransform()));
log.message("world transformation matrix of the child node: %s\n", typeinfo(box_2.getWorldTransform()));
return 1;
}After running this code, we get the following result:
transformation matrix of the child node: dmat4: (1 0 0 0) (0 1 0 0) (0 0 1 0) (0 2 1 1)
world transformation matrix of the child node: dmat4 (1 0 0 0) (0 1 0 0) (0 0 1 0) (0 2 1 1)The matrices are the same, since the parent node box_1 has the zero transformation (0,0,0). It means that its origin and the world origin are coincident. If we change the transformation of the first mesh to another, for example:
mat4 transform = translate(vec3(2.0f,2.0f,2.0f));We get another result:
transformation matrix of the child node: dmat4: (1 0 0 0) (0 1 0 0) (0 0 1 0) (0 2 1 1)
world transformation matrix of the child node: dmat4 (1 0 0 0) (0 1 0 0) (0 0 1 0) (2 4 3 1)As you see, the local transformation matrix remains the same but the world transformation matrix has been changed. This means that the second node has the same position relative to the first, but another position relative to the world origin because the position of the parent node has been changed.

|

|
|
Parent node's origin coincides with the world origin
|
Parent node has been moved and child node has also been moved automatically
|