Math Matrix Functions
| Header: | #include <UnigineMathLib.h> |
Math Class
Members
mat4 composeRotationXYZ ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - XYZ. It is an order of the rings in the three-axis gimbal set: X axis used as the outer ring (independent ring), while Z axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 composeRotationXZY ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - XZY. It is an order of the rings in the three-axis gimbal set: X axis used as the outer ring (independent ring), while Y axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 composeRotationYXZ ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - YXZ. It is an order of the rings in the three-axis gimbal set: Y axis used as the outer ring (independent ring), while Z axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 composeRotationYZX ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - YZX. It is an order of the rings in the three-axis gimbal set: Y axis used as the outer ring (independent ring), while X axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 composeRotationZXY ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - ZXY. It is an order of the rings in the three-axis gimbal set: Z axis used as the outer ring (independent ring), while Y axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 composeRotationZYX ( const vec3 & r ) #
Composes a rotation matrix from the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - ZYX. It is an order of the rings in the three-axis gimbal set: Z axis used as the outer ring (independent ring), while X axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const vec3 & r - Vector, containing Euler angles, in degrees - (yaw, roll, pitch).
Return value
Composed rotation matrix.mat4 & composeTransform ( mat4 & ret, const vec4 & position, const quat & rot ) #
Returns the transformation matrix for the specified position and rotation.Arguments
- mat4 & ret - Output matrix, to which the resulting transformation matrix will be put.
- const vec4 & position
- const quat & rot - Rotation quaternion.
Return value
Resulting transformation matrix.mat4 & composeTransform ( mat4 & ret, const vec3 & position, const quat & rot, const vec3 & scale ) #
Returns the transformation matrix for the specified position, rotation and scale. For more information see Matrix Transformations.Arguments
- mat4 & ret - Output matrix, to which the resulting transformation matrix will be put.
- const vec3 & position - Position coordinates (world).
- const quat & rot - Rotation quaternion.
- const vec3 & scale - Scaling vector (scale.x, scale.y, scale.z).
Return value
Resulting transformation matrix.dmat4 & composeTransform ( dmat4 & ret, const dvec3 & position, const quat & rot, const vec3 & scale ) #
Returns the transformation matrix for the specified position, rotation and scale. For more information see Matrix Transformations.Arguments
- dmat4 & ret - Output matrix, to which the resulting transformation matrix will be put.
- const dvec3 & position
- const quat & rot - Rotation quaternion.
- const vec3 & scale - Scaling vector (scale.x, scale.y, scale.z).
Return value
Resulting transformation matrix.mat4 & composeTransform ( mat4 & ret, const quat & q0, const quat & q1, const vec3 & scale ) #
Returns the transformation matrix for the specified position, rotation and scale. For more information see Matrix Transformations.Arguments
- mat4 & ret - Output matrix, to which the resulting transformation matrix will be put.
- const quat & q0
- const quat & q1
- const vec3 & scale - Scaling vector (scale.x, scale.y, scale.z).
Return value
Resulting transformation matrix.mat4 cubeTransform ( int face ) #
Returns cube viewing matrix for the given cube face.Arguments
- int face - Cube face number.
Return value
Cube viewing matrix.float decomposePerspectiveFov ( const mat4 & projection ) #
Decomposes a given perspective projection matrix, extracting the field of view angle.Arguments
- const mat4 & projection - Perspective projection matrix.
Return value
Field of view angle.void decomposeProjection ( const mat4 & projection, float & znear, float & zfar ) #
Decomposes a given projection matrix, extracting distances to near and far clipping planes.Arguments
- const mat4 & projection - Projection matrix.
- float & znear - Near clipping plane.
- float & zfar - Far clipping plane.
void decomposeProjection ( const mat4 & projection, float & znear, float & zfar, float & fov ) #
Decomposes a given projection matrix, extracting distances to near and far clipping planes, and the field of view angle.Arguments
- const mat4 & projection - Projection matrix.
- float & znear - Near clipping plane.
- float & zfar - Far clipping plane.
- float & fov - Field of view angle.
vec3 decomposeRotationXYZ ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - XYZ. It is an order of the rings in the three-axis gimbal set: X axis used as the outer ring (independent ring), while Z axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (pitch, roll, yaw).vec3 decomposeRotationXZY ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - XZY. It is an order of the rings in the three-axis gimbal set: X axis used as the outer ring (independent ring), while Y axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (pitch, yaw, roll).vec3 decomposeRotationYXZ ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - YXZ. It is an order of the rings in the three-axis gimbal set: Y axis used as the outer ring (independent ring), while Z axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (roll, pitch, yaw).vec3 decomposeRotationYZX ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - YZX. It is an order of the rings in the three-axis gimbal set: Y axis used as the outer ring (independent ring), while X axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (roll, yaw, pitch).vec3 decomposeRotationZXY ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - ZXY. It is an order of the rings in the three-axis gimbal set: Z axis used as the outer ring (independent ring), while Y axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (yaw, pitch, roll).vec3 decomposeRotationZYX ( const mat3 & t ) #
Decomposes a given rotation matrix to the corresponding Euler angles. The Euler angles are specified in the axis rotation sequence - ZYX. It is an order of the rings in the three-axis gimbal set: Z axis used as the outer ring (independent ring), while X axis as the inner one (its rotation depends on other 2 rings).
When we talk about axes in UNIGINE we assume that:
- X axis points to the right giving us a pitch angle.
- Y axis points forward giving us a roll angle.
- Z axis points up giving us a yaw (heading) angle.
- X axis points to the right giving us a pitch angle.
- Y axis points up giving us a yaw (heading) angle.
- Z axis points backward giving us a -roll angle.
Arguments
- const mat3 & t - Rotation matrix to decompose.
Return value
Vector, containing Euler angles, in degrees - (yaw, roll, pitch).void decomposeTransform ( const mat4 & m, vec4 & position, quat & rot ) #
Decomposes a given transformation matrix into a vector representing translation and uniform scale and a quaternion representing rotation.Arguments
- const mat4 & m - Transformation matrix to decompose.
- vec4 & position - Output vector (X, Y, Z, W), to which translation and scale components of the transformation will be put. (X, Y, Z) - represent translation, W = (scale.X + scale.Y + scale.z) / 3.
- quat & rot - Output quaternion, to which the rotation component of the transformation will pe put.
void decomposeTransform ( const mat4 & m, vec3 & position, quat & rot, vec3 & scale ) #
Decomposes a given transformation matrix into translation, rotation and scale components.Arguments
- const mat4 & m - Transformation matrix to decompose.
- vec3 & position - Output vector, to which the translation component of the transformation will be put.
- quat & rot - Output quaternion, to which the rotation component of the transformation will be put.
- vec3 & scale - Output vector, to which the scale component of the transformation will be put.
void decomposeTransform ( const dmat4 & m, dvec3 & position, quat & rot, vec3 & scale ) #
Decomposes a given transformation matrix into translation, rotation and scale components.Arguments
- const dmat4 & m - Transformation matrix to decompose.
- dvec3 & position - Output vector, to which the translation component of the transformation will be put.
- quat & rot - Output quaternion, to which the rotation component of the transformation will be put.
- vec3 & scale - Output vector, to which the scale component of the transformation will be put.
void decomposeTransform ( const mat4 & m, quat & q0, quat & q1, vec3 & scale ) #
Decomposes a given transformation matrix into a dual quaternion (representing both translation and rotation) and a scale vector. The dual-quaternion model is an accurate, computationally efficient, robust, and flexible method of representing rigid transforms and it is used in skeletal animation. See a Wikipedia article on dual quaternions and a beginners guide to dual-quaternions for more information.Arguments
- const mat4 & m - Transformation matrix to decompose.
- quat & q0 - Quaternion representing a real part of the dual quaternion.
- quat & q1 - Quaternion representing a dual part of the dual quaternion.
- vec3 & scale - Scale part of the transformation.
float determinant ( const mat2 & m ) #
Returns the determinant of the given matrix.Arguments
- const mat2 & m - Matrix, for which the determinant is to be calculated.
Return value
Matrix determinant.float determinant ( const mat3 & m ) #
Returns the determinant of the given matrix.Arguments
- const mat3 & m - Matrix, for which the determinant is to be calculated.
Return value
Matrix determinant.float determinant ( const mat4 & m ) #
Returns the determinant of the given matrix.Arguments
- const mat4 & m - Matrix, for which the determinant is to be calculated.
Return value
Matrix determinant.double determinant ( const dmat4 & m ) #
Returns the determinant of the given matrix.Arguments
- const dmat4 & m - Matrix, for which the determinant is to be calculated.
Return value
Matrix determinant.mat4 frustum ( float left, float right, float bottom, float top, float znear, float zfar ) #
Returns perspective projection matrix:| 2.0 * znear / (right - left) | 0.0 | (right + left) / (right - left) | 0.0 |
| 0.0 | 2.0 * znear / (top - bottom) | (top + bottom) / (top - bottom) | 0.0 |
| 0.0 | 0.0 | -(zfar + znear) / (zfar - znear) | -2.0 * zfar * znear / (zfar - znear) |
| 0.0 | 0.0 | -1.0 | 0.0 |
Coordinates of top, left, right, bottom are set relatively to center point of the znear plane.
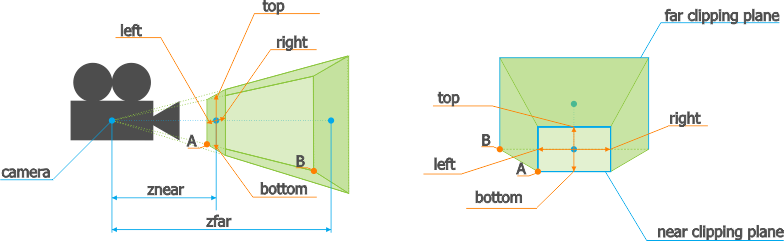
There are two different points (A and B) on the picture above. Since the top, left, right, bottom are coordinates relatively to the center point of the znear plane, coordinates of the A point should be A(left, bottom, znear). Coordinates of the B point are B(k * left, k * bottom, zfar), where k = zfar/znear.
Arguments
- float left - Left coordinate of the near clipping plane relatively to the center.
- float right - Right coordinate of the near clipping plane relatively to the center.
- float bottom - Bottom coordinate of the near clipping plane relatively to the center.
- float top - Top coordinate of the near clipping plane relatively to the center.
- float znear - Distance to the near depth clipping plane.
- float zfar - Distance to the farther depth clipping plane.
Return value
Perspective projection matrix.mat2 inverse ( const mat2 & m ) #
Returns inverse of a matrix. The inverse of a matrix is a matrix that if multiplied by the original would result in identity matrix: AA -1 = A -1A = I.Arguments
- const mat2 & m - Matrix to be inverted.
Return value
Inverse of the matrix.mat3 inverse ( const mat3 & m ) #
Returns inverse of a matrix. The inverse of a matrix is a matrix that if multiplied by the original would result in identity matrix: AA -1 = A -1A = I.Arguments
- const mat3 & m - Matrix to be inverted.
Return value
Inverse of the matrix.dmat4 inverse ( const dmat4 & m ) #
Returns inverse of a matrix. The inverse of a matrix is a matrix that if multiplied by the original would result in identity matrix: AA -1 = A -1A = I.Arguments
- const dmat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.dmat4 inverse ( dmat4 & ret, const dmat4 & m ) #
Returns inverse of a matrix. The inverse of a matrix is a matrix that if multiplied by the original would result in identity matrix: AA -1 = A -1A = I.Arguments
- dmat4 & ret - Output matrix, to which the inverted matrix will be put.
- const dmat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.mat4 inverse ( const mat4 & m ) #
Returns inverse of a matrix. The inverse of a matrix is a matrix that if multiplied by the original would result in identity matrix: AA -1 = A -1A = I.Arguments
- const mat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.quat inverse ( const quat & q ) #
Returns inverse of a quaternion. The inverse of a quaternion is a quaternion that if multiplied by the original would result in identity matrix: qq -1 = 1. If q = a + bi + cj + dk, then q-1 = a - bi - cj - dkArguments
- const quat & q - Quaternion to be inverted.
Return value
Inverse of the quaternion.mat4 inverse4 ( const mat4 & m ) #
Inverts a matrix that consists of a 3×4 sub-matrix (upper left) and a translation vector. The last row of the matrix is ignored. Compared to the inverse() function, this one is a bit faster and, which is more important, more stable. A matrix suitable for such inversion looks like this:| m00 | m10 | m20 | m30 |
| m01 | m11 | m21 | m31 |
| m02 | m12 | m22 | m32 |
| 0 | 0 | 0 | 1 |
Arguments
- const mat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.dmat4 inverse4 ( const dmat4 & m ) #
Inverts a matrix that consists of a 3×4 sub-matrix (upper left) and a translation vector. The last row of the matrix is ignored. Compared to the inverse() function, this one is a bit faster and, which is more important, more stable. A matrix suitable for such inversion looks like this:| m00 | m10 | m20 | m30 |
| m01 | m11 | m21 | m31 |
| m02 | m12 | m22 | m32 |
| 0 | 0 | 0 | 1 |
Arguments
- const dmat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.dmat4 & inverse4 ( dmat4 & ret, const dmat4 & m ) #
Inverts a matrix that consists of a 3×4 sub-matrix (upper left) and a translation vector. The last row of the matrix is ignored. Compared to the inverse() function, this one is a bit faster and, which is more important, more stable. A matrix suitable for such inversion looks like this:| m00 | m10 | m20 | m30 |
| m01 | m11 | m21 | m31 |
| m02 | m12 | m22 | m32 |
| 0 | 0 | 0 | 1 |
Arguments
- dmat4 & ret - Output matrix, to which the orthonormalized matrix will be put.
- const dmat4 & m - Matrix to be inverted.
Return value
Inverse of the matrix.mat3 jacobi ( const mat3 & m, mat3 & v ) #
Returns the Jacobian matrix for the given 3x3 matrix.Arguments
- const mat3 & m - Matrix, for which the Jacobian matrix is to be calculated.
- mat3 & v - Output matrix, to which the calculated Jacobian matrix will be put.
Return value
Jacobian matrix.mat4 lookAt ( const vec3 & position, const vec3 & target, const vec3 & up, int axis = AXIS_NZ ) #
Returns the viewing matrix for the given eye point, target point, up and forward direction vectors. The forward direction vector is pointed along the specified axis. By default, it is negative Z.Arguments
- const vec3 & position - Position coordinates of the eye point.
- const vec3 & target - Position of the target point.
- const vec3 & up - Direction of the up vector.
- int axis - Axis along which the forward direction vector is pointed. The default is negative Z.
Return value
The viewing matrix.dmat4 lookAt ( const dvec3 & position, const dvec3 & target, const vec3 & up, int axis = AXIS_NZ ) #
Returns the viewing matrix for the given eye point, target point, up and forward direction vectors. The forward direction vector is pointed along the specified axis. By default, it is negative Z.Arguments
- const dvec3 & position - Position coordinates of the eye point.
- const dvec3 & target - Position coordinates of the target point.
- const vec3 & up - Direction of the up vector.
- int axis - Axis along which the forward direction vector is pointed. The default is negative Z.
Return value
The viewing matrix.mat4 obliqueProjection ( const mat4 & projection, const vec4 & plane ) #
Returns the oblique projection matrix.Arguments
Return value
Oblique projection matrix.quat orthoTangent ( const vec4 & tangent, const vec3 & normal ) #
Creates the ortho triangle tangent space basis.Arguments
Return value
The tangent basis.quat orthoTangent ( const vec3 & tangent, const vec3 & binormal, const vec3 & normal ) #
Creates the ortho triangle tangent space basis.Arguments
- const vec3 & tangent - Tangent vector.
- const vec3 & binormal - Binormal vector.
- const vec3 & normal - Normal vector.
Return value
The tangent basis.mat4 ortho ( float left, float right, float bottom, float top, float znear, float zfar ) #
Returns parallel projection matrix:| 2.0 / (right - left) | 0.0 | 0.0 | -(right + left) / (right - left) |
| 0.0 | 2.0 / (top - bottom) | 0.0 | -(top + bottom) / (top - bottom) |
| 0.0 | 0.0 | -2.0 / (zfar - znear) | -(zfar + znear) / (zfar - znear) |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float left - Left vertical clipping plane.
- float right - Right vertical clipping plane.
- float bottom - Bottom horizontal clipping plane.
- float top - Top horizontal clipping plane.
- float znear - Nearest depth clipping plane.
- float zfar - Farther depth clipping plane.
Return value
Parallel projection matrix.mat3 orthonormalize ( const mat3 & m ) #
Orthonormalizes a matrix.Arguments
- const mat3 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.mat4 orthonormalize ( const mat4 & m ) #
Orthonormalizes a matrix.Arguments
- const mat4 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.dmat4 orthonormalize ( const dmat4 & m ) #
Orthonormalizes a matrix.Arguments
- const dmat4 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.mat3 & orthonormalize ( mat3 & ret, const mat3 & m ) #
Orthonormalizes a matrix.Arguments
- mat3 & ret - Output matrix, to which the orthonormalized matrix will be put.
- const mat3 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.mat4 & orthonormalize ( mat4 & ret, const mat4 & m ) #
Orthonormalizes a matrix.Arguments
- mat4 & ret - Output matrix, to which the orthonormalized matrix will be put.
- const mat4 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.dmat4 & orthonormalize ( dmat4 & ret, const dmat4 & m ) #
Orthonormalizes a matrix.Arguments
- dmat4 & ret - Output matrix, to which the orthonormalized matrix will be put.
- const dmat4 & m - Matrix to be orthonormalized.
Return value
Orthonormal matrix.mat4 perspective ( float fov, float aspect, float znear, float zfar ) #
Returns perspective projection matrix.Arguments
- float fov - Field of view angle.
- float aspect - Aspect ratio. The aspect ratio is the ratio of width to height.
- float znear - Nearest depth clipping plane.
- float zfar - Farther depth clipping plane.
Return value
Perspective projection matrix.mat4 reflect ( const vec4 & plane ) #
Returns reflection matrix about a given plane.Arguments
- const vec4 & plane - Reflection plane.
Return value
Reflection matrix.dmat4 reflect ( const dvec4 & plane ) #
Returns reflection matrix about a given plane.Arguments
- const dvec4 & plane - Reflection plane.
Return value
Reflection matrix.vec3 reflect ( const vec3 & v0, const vec3 & v1 ) #
Reflects a given vector about a plane with the specified normal vector.Arguments
Return value
Reflected vector.dvec3 reflect ( const dvec3 & v0, const dvec3 & v1 ) #
Reflects a given vector about a plane with the specified normal vector.Arguments
Return value
Reflected vector.vec3 & reflect ( vec3 & ret, const vec3 & v0, const vec3 & v1 ) #
Reflects a given vector about a plane with the specified normal vector.Arguments
- vec3 & ret - Reflected vector.Output vector, to which the reflected vector will be put.
- const vec3 & v0 - Vector to be reflected.
- const vec3 & v1 - Normal vector to the reflection plane.
Return value
Reflected vector.dvec3 & reflect ( dvec3 & ret, const dvec3 & v0, const dvec3 & v1 ) #
Reflects a given vector about a plane with the specified normal vector.Arguments
- dvec3 & ret - Output vector, to which the reflected vector will be put.
- const dvec3 & v0 - Vector to be reflected.
- const dvec3 & v1 - Normal vector to the reflection plane.
Return value
Reflected vector.mat4 & removeScale ( mat4 & ret, vec3 & scale ) #
Resets the transformation scale by replacing the scale component of the transformation matrix with a vec3_one (vector filled with ones). The original scale is stored in the vector argument.Arguments
- mat4 & ret - Matrix to store the output.
- vec3 & scale - Vector to store the scale component of the transformation.
Return value
Output matrix.mat4 & removeScale ( mat4 & ret ) #
Resets the transformation scale by replacing the scale component of the transformation matrix with a vec3_one (vector filled with ones).Arguments
- mat4 & ret - Matrix to store the output.
Return value
Output matrix.dmat4 & removeScale ( dmat4 & ret, vec3 & scale ) #
Resets the transformation scale by replacing the scale component of the transformation matrix with a vec3_one (vector filled with ones). The original scale is stored in the vector argument.Arguments
- dmat4 & ret - Matrix to store the output.
- vec3 & scale - Vector to store the scale component of the transformation.
Return value
Output matrix.dmat4 & removeScale ( dmat4 & ret ) #
Resets the transformation scale by replacing the scale component of the transformation matrix with a vec3_one (vector filled with ones).Arguments
- dmat4 & ret - Matrix to store the output.
Return value
Output matrix.mat4 rotateX ( float angle ) #
Returns rotation matrix for the given angle around X axis:| 1.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | cos | -sin | 0.0 |
| 0.0 | sin | cos | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float angle - Rotation angle, in degrees.
Return value
Rotation matrix.dmat4 rotateX ( double angle ) #
Returns the X rotation matrix.Arguments
- double angle - Rotation angle, in degrees.
Return value
Rotation matrix.mat4 rotateY ( float angle ) #
Returns rotation matrix for the given angle around Y axis:| cos | 0.0 | sin | 0.0 |
| 0.0 | 1.0 | 0.0 | 0.0 |
| -sin | 0.0 | cos | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float angle - Rotation angle, in degrees.
Return value
Rotation matrix.dmat4 rotateY ( double angle ) #
Returns the Y rotation matrix.Arguments
- double angle - Rotation angle, in degrees.
Return value
Rotation matrix.mat4 rotateZ ( float angle ) #
Returns rotation matrix for the given angle around Z axis:| cos | -sin | 0.0 | 0.0 |
| sin | cos | 0.0 | 0.0 |
| 0.0 | 0.0 | 1.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float angle - Rotation angle, in degrees.
Return value
Rotation matrix.dmat4 rotateZ ( double angle ) #
Returns the Z rotation matrix.Arguments
- double angle - Rotation angle, in degrees.
Return value
Rotation matrix.dmat4 rotate ( double x, double y, double z, double angle ) #
Returns rotation matrix for the given angle around the given axis (X, Y, Z).Arguments
- double x - X component of rotation axis.
- double y - Y component of rotation axis.
- double z - Z component of rotation axis.
- double angle - Rotation angle, in degrees.
Return value
Rotation matrix.mat4 rotate ( float x, float y, float z, float angle ) #
Returns rotation matrix for the given angle around the given axis (X, Y, Z).Arguments
- float x - X component of rotation axis.
- float y - Y component of rotation axis.
- float z - Z component of rotation axis.
- float angle - Rotation angle, in degrees.
Return value
Rotation matrix.mat4 rotate ( const quat & q ) #
Returns rotation matrix for the given quaternion.Arguments
- const quat & q - Rotation quaternion.
Return value
Rotation matrix.mat4 rotate ( const vec3 & axis, float angle ) #
Returns rotation matrix.Arguments
- const vec3 & axis - Rotation axis. This vector does not have to be normalized.
- float angle - Rotation angle, in degrees.
Return value
Rotation matrix.dmat4 rotate ( const dvec3 & axis, double angle ) #
Returns rotation matrix for the given angle around the given axis (X, Y, Z).Arguments
- const dvec3 & axis - Rotation axis. This vector does not have to be normalized.
- double angle - Rotation angle, in degrees.
Return value
Rotation matrix.quat rotateTowards ( const quat & source, const quat & target, float max_angle ) #
Rotates the source quaternion towards the target quaternion by an angular step of max_angle (note, that the rotation will not overshoot).Arguments
- const quat & source - Source quaternion.
- const quat & target - Target quaternion.
- float max_angle - Angular step, in degrees. If a negative value is specified, 0 will be used instead.
Return value
Resulting quaternion.vec3 rotateTowards ( const vec3 & source, const vec3 & target, float max_angle ) #
Rotates the source vector towards the target vector by an angular step of max_angle (note, that the rotation will not overshoot).Arguments
- const vec3 & source - Source vector.
- const vec3 & target - Target vector.
- float max_angle - Angular step, in degrees. If a negative value is specified, 0 will be used instead.
Return value
Resulting vector.mat4 rotation ( const mat4 & m ) #
Returns the rotation matrix for the given source matrix ignoring the translation column. For more information see Matrix Transformations.Arguments
- const mat4 & m - Source matrix.
Return value
Rotation matrix.dmat4 rotation ( const dmat4 & m ) #
Returns the rotation matrix for the given source matrix ignoring the translation column. For more information see Matrix Transformations.Arguments
- const dmat4 & m - Source matrix.
Return value
Rotation matrix.mat4 & rotation ( mat4 & ret, const mat4 & m ) #
Returns the rotation matrix for the given source matrix ignoring the translation column. For more information see Matrix Transformations.Arguments
- mat4 & ret - Output matrix, to which the rotation matrix will be put.
- const mat4 & m - Source matrix.
Return value
Rotation matrix.dmat4 & rotation ( dmat4 & ret, const dmat4 & m ) #
Returns the rotation matrix for the given source matrix ignoring the translation column. For more information see Matrix Transformations.Arguments
- dmat4 & ret - Output matrix, to which the rotation matrix will be put.
- const dmat4 & m - Source matrix.
Return value
Rotation matrix.quat rotationFromDir ( const vec3 & forward, const vec3 & up ) #
Returns the rotation quaternion for the specified "forward" and "up" directions. For more information see Matrix Transformations.Arguments
- const vec3 & forward - Forward direction vector defining the direction to look in.
- const vec3 & up - Vector defining in which direction up is.
Return value
Rotation quaternion.quat rotationFromDir ( const vec3 & forward ) #
Returns the rotation quaternion for the specified "forward" direction (the default "up" vector is used). For more information see Matrix Transformations.Arguments
- const vec3 & forward - Forward direction vector defining the direction to look in.
Return value
Rotation quaternion.quat rotationFromTo ( const vec3 & from_dir, const vec3 & to_dir ) #
Returns the rotation quaternion for the specified source and target directions. For more information see Matrix Transformations.Arguments
- const vec3 & from_dir - Vector defining the initial direction.
- const vec3 & to_dir - Vector defining the target direction.
Return value
Rotation quaternion.mat4 scale ( float x, float y, float z ) #
Returns scaling matrix for the specified scaling vector (X, Y, Z):| X | 0.0 | 0.0 | 0.0 |
| 0.0 | Y | 0.0 | 0.0 |
| 0.0 | 0.0 | Z | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float x - X component of the scaling vector.
- float y - Y component of the scaling vector.
- float z - Z component of the scaling vector.
Return value
Scaling matrix.dmat4 scale ( double x, double y, double z ) #
Returns scaling matrix for the specified scaling vector (X, Y, Z):| X | 0.0 | 0.0 | 0.0 |
| 0.0 | Y | 0.0 | 0.0 |
| 0.0 | 0.0 | Z | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- double x - X component of the scaling vector.
- double y - Y component of the scaling vector.
- double z - Z component of the scaling vector.
Return value
Scaling matrix.mat4 scale ( const vec3 & v ) #
Returns the scaling matrix for the specified scaling vector (X, Y, Z):| X | 0.0 | 0.0 | 0.0 |
| 0.0 | Y | 0.0 | 0.0 |
| 0.0 | 0.0 | Z | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- const vec3 & v - Scaling vector.
Return value
Scaling matrix.dmat4 scale ( const dvec3 & v ) #
Returns the scaling matrix for the specified scaling vector (X, Y, Z):| X | 0.0 | 0.0 | 0.0 |
| 0.0 | Y | 0.0 | 0.0 |
| 0.0 | 0.0 | Z | 0.0 |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- const dvec3 & v - Scaling vector.
Return value
Scaling matrix.dmat4 setTo ( const dvec3 & position, const dvec3 & target, const vec3 & up, int axis = AXIS_NZ ) #
Returns the transformation matrix, which puts an object to the specified position and sets it orientation to the specified target point. At that, the forward direction vector is pointed along the specified axis. By default, it is negative Z.Arguments
- const dvec3 & position - Position of the eye point.
- const dvec3 & target - Position of the target point.
- const vec3 & up - Direction of the up vector.
- int axis - Axis along which the forward direction vector is pointed. The default is negative Z.
Return value
Transformation matrix.mat4 setTo ( const vec3 & position, const vec3 & target, const vec3 & up, int axis = AXIS_NZ ) #
Returns the transformation matrix, which puts an object to the specified position and sets it orientation to the specified target point. At that, the forward direction vector is pointed along the specified axis. By default, it is negative Z.Arguments
- const vec3 & position - Position of the eye point.
- const vec3 & target - Position of the target point.
- const vec3 & up - Direction of the up vector.
- int axis - Axis along which the forward direction vector is pointed. The default is negative Z.
Return value
Transformation matrix.mat4 symmetryProjection ( const mat4 & projection ) #
Returns the symmetry projection matrix.Arguments
- const mat4 & projection - Projection matrix.
Return value
The symmetry projection matrix.mat4 translate ( float x, float y, float z ) #
Returns the translation matrix for the specified translation vector (X, Y, Z):| 1.0 | 0.0 | 0.0 | X |
| 0.0 | 1.0 | 0.0 | Y |
| 0.0 | 0.0 | 1.0 | Z |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- float x - X component of the translation vector.
- float y - Y component of the translation vector.
- float z - Z component of the translation vector.
Return value
Translation matrix.dmat4 translate ( double x, double y, double z ) #
Returns the translation matrix for the specified translation vector (X, Y, Z):| 1.0 | 0.0 | 0.0 | X |
| 0.0 | 1.0 | 0.0 | Y |
| 0.0 | 0.0 | 1.0 | Z |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- double x - X component of the translation vector.
- double y - Y component of the translation vector.
- double z - Z component of the translation vector.
Return value
Translation matrix.mat4 translate ( const vec3 & v ) #
Returns the translation matrix for the specified translation vector (X, Y, Z):| 1.0 | 0.0 | 0.0 | X |
| 0.0 | 1.0 | 0.0 | Y |
| 0.0 | 0.0 | 1.0 | Z |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- const vec3 & v - Translation vector.
Return value
Translation matrix.dmat4 translate ( const dvec3 & v ) #
Returns the translation matrix for the specified translation vector (X, Y, Z):| 1.0 | 0.0 | 0.0 | X |
| 0.0 | 1.0 | 0.0 | Y |
| 0.0 | 0.0 | 1.0 | Z |
| 0.0 | 0.0 | 0.0 | 1.0 |
Arguments
- const dvec3 & v - Translation vector.
Return value
Translation matrix.mat2 transpose ( const mat2 & m ) #
Transposes a given 2x2 matrix.Arguments
- const mat2 & m - Matrix to be transposed.
Return value
Transposed matrix.mat2 & transpose ( mat2 & ret, const mat2 & m ) #
Transposes a given 2x2 matrix.Arguments
- mat2 & ret - Output matrix, to which the transposed matrix will be put.
- const mat2 & m - Matrix to be transposed.
Return value
Transposed matrix.mat3 transpose ( const mat3 & m ) #
Transposes a given 3x3 matrix.Arguments
- const mat3 & m - Matrix to be transposed.
Return value
Transposed matrix.mat3 & transpose ( mat3 & ret, const mat3 & m ) #
Transposes a given 3x3 matrix.Arguments
- mat3 & ret - Output matrix, to which the transposed matrix will be put.
- const mat3 & m - Matrix to be transposed.
mat4 transpose ( const mat4 & m ) #
Transposes a given 4x4 matrix.Arguments
- const mat4 & m - Matrix to be transposed.
Return value
Transposed matrix.mat4 & transpose ( mat4 & ret, const mat4 & m ) #
Transposes a given 4x4 matrix.Arguments
- mat4 & ret - Output matrix, to which the transposed matrix will be put.
- const mat4 & m - Matrix to be transposed.
Return value
Transposed matrix.mat4 transpose3 ( const mat4 & m ) #
Transposes the upper left 3×3 sub-matrix of a matrix.Arguments
- const mat4 & m - Matrix, a part of which will be transposed.
Return value
Matrix, in which the upper left 3×3 sub-matrix is transposed.mat4 & transpose3 ( mat4 & ret, const mat4 & m ) #
Transposes the upper left 3×3 sub-matrix of a matrix.Arguments
- mat4 & ret - Output matrix, to which the resulting matrix will be put.
- const mat4 & m - Matrix, a part of which will be transposed.