Matrix Transformations
A lot of calculations in Unigine are performed by using matrices. Actually, matrix transformations are one of the main concepts of 3D engines. This article contains an explanation of matrix transformations with usage examples.
See Also
Transformations
In simple terms, a matrix in 3D graphics is an array of numbers arranged in rows and columns:

Usually, 4x4 matrices are used. Such size (4x4) of matrices is caused by the translation state in 3D space. When you put a new node into the world, it has a 4x4 world transform matrix that defines the position of the node in the world.
In Unigine, matrices are column major (column-oriented). Hence, the first column of the transform matrix represent the X vector v1, the second represent Y vector v2, the third represent Z vector v3, and the fourth represent the translation vector t. First three columns show directions of axes and the scale of the origin. The last column contains the translation of the local origin relatively to the world origin.
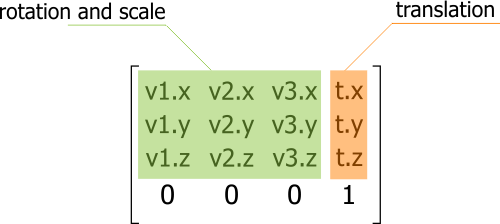
Identity Matrix
The world origin has the following matrix:

This matrix is called identity matrix, a matrix with ones on the main diagonal, and zeros elsewhere. If a matrix will be multiplied by the identity matrix, it won't change anything: the resulting matrix will be the same as it was before multiplying.
If the local origin has the identity matrix, it means the local origin and the world origin are coincident.
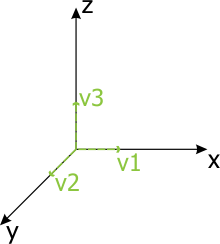
Rotation
To change the orientation of the local origin, the first three columns of the matrix should be changed.
To rotate the origin along different axes, you should use proper matrices:
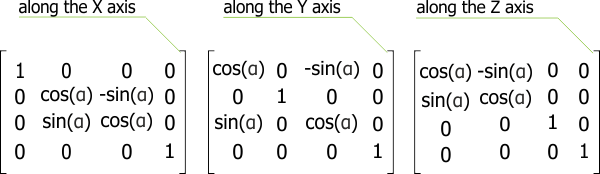
In the matrices given above, α is a rotation angle along the axis.
The next matrix shows the rotation of the local origin along the Y axis at 45 degrees:
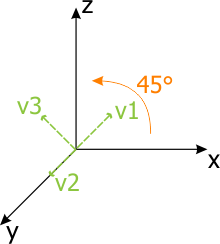
|

|
Translation
The last column of the transform matrix shows the position of the local origin in the world relatively to the world origin. The next matrix shows the translation of the origin. The translation vector t is (3, 0, 2).

|
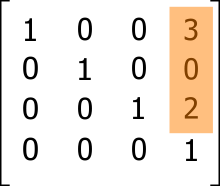
|
Scaling
The length of the vector shows the scale coefficient along the axis.
To calculate the vector length (also known as magnitude), you should find a square root of the sum of the squares of vector components. The formula is the following:
|vector length| = √(x² + y² + z²)The following matrix scales the local origin up to 2 units along all axes.
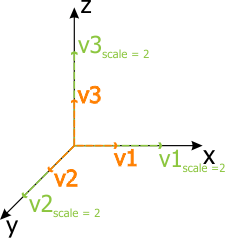
|

|
Cumulating Transformations
The order of matrix transformations (scaling, rotation and translation) is very important.
The order of cumulating transformations is the following:
- Translation
- Rotation
- Scaling
This is the formula of the transformation order:
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * VectorHere is an example which demonstrates different positions of the local origin related to the world origin.
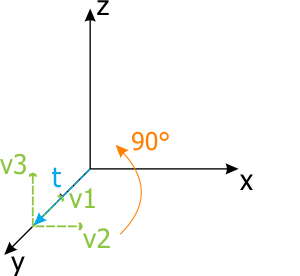
|
|
|
Translation * Rotation order
|
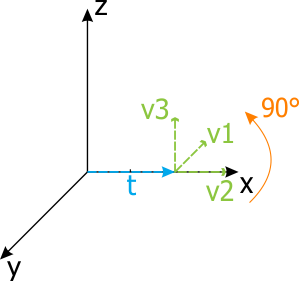
Rotation * Translation order
|
On the left picture, the local origin was translated first and then rotated; on the right picture, the local origin was rotated first and then translated. All values (rotation angle, translation vector) are the same, but the result is different.
Example
This example shows what happens if you choose another order of matrix transformations.
The code example below gets the material ball object. In the first case we use the translation * rotation order, in the second case we use the rotation * translation order.
In the AppWorldLogic.h file, define the material_ball node smart pointer.
// AppWorldLogic.h
/* ... */
class AppWorldLogic : public Unigine::WorldLogic {
public:
/* .. */
private:
Unigine::NodePtr material_ball;
};In the AppWorldLogic.cpp file, perform the following:
- Include the UnigineEditor.h, UnigineVisualizer.h, UnigineConsole.h headers.
- Use using namespace Unigine and using namespace Unigine::Math directives: names of the Unigine and Unigine::Math namespaces will be injected into global namespace.
- Enable the visualizer by passing show_visualizer 1 command to the run() function of the Console class.
- Get the material ball from the Editor.
- Create new rotation and translation matrices.
- Calculate new transformation matrix and apply it to the material ball.
- Render the world origin by using renderVector() method of the Visualizer class.
// AppWorldLogic.cpp file
#include "AppWorldLogic.h"
#include "UnigineEditor.h"
#include "UnigineVisualizer.h"
#include "UnigineConsole.h"
// inject Unigine and Unigine::Math namespaces names to global namespace
using namespace Unigine;
using namespace Unigine::Math;
/* ... */
int AppWorldLogic::init() {
// enable the visualizer for world origin rendering
Console::get()->run("show_visualizer 1");
// get the material ball from editor
material_ball = Editor::get()->getNodeByName("material_ball");
// create rotation and translation matrices
Mat4 rotation_matrix = (Mat4)rotateZ(-90.0f);
Mat4 translation_matrix = (Mat4)translate(vec3(0.0f, 3.0f, 0.0f));
// create a new transformation matrix for the material ball
// by multiplying the current matrix by rotation and translation matrices
Mat4 transform = material_ball->getTransform() * translation_matrix * rotation_matrix;
// set the transformation matrix to the material ball
material_ball->setTransform(transform);
return 1;
}
int AppWorldLogic::update() {
// render world origin
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(1.0f,0.0f,0.1f), vec4(1.0f,0.0f,0.0f,1.0f));
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(0.0f,1.0f,0.1f), vec4(0.0f,1.0f,0.0f,1.0f));
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(0.0f,0.0f,1.1f), vec4(0.0f,0.0f,1.0f,1.0f));
return 1;
}To change the order, just change the line of cumulating transformations:
Mat4 transform = material_ball->getTransform() * rotation_matrix * translation_matrix;The result will be different. The pictures below show the difference (camera is located at the same place).

|

|
|
Translation * Rotation order
|
Rotation * Translation order
|
The pictures above show the position of the meshes related to the world origin.
Matrix Hierarchy
Another important concept is a matrix hierarchy. When a node is added into the world as a child of another node, it has a transform matrix that is related to the parent node. That is why the Node class has different functions: getTransform(), setTransform() and getWorldTransform(), setWorldTransform() that return the local and the world transformation matrices respectively.
What is the reason of using matrix hierarchy? To move a node relatively to another node. And when you move a parent node, child nodes will also be moved, that is the point.
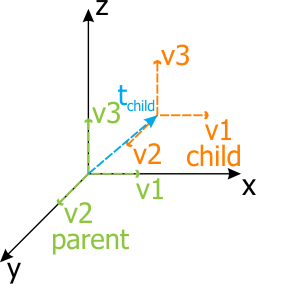
|
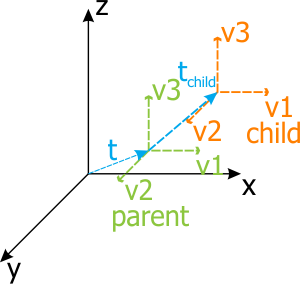
|
|
Parent origin is the same with the world origin
|
Parent origin has been moved and the child origin has also been moved
|
Pictures above show the main point of the matrix hierarchy. When the parent origin (node) is moved, the chlld origin will also be moved and the local transformation matrix of the child would not be changed. But the world transformation matrix of the child will be changed. If you need the world transformation matrix of the child related to the world origin, you should use the getWorldTransform(), setWorldTransform() functions; in case, when you need the local transformation matrix of the child related to the parent, you should use the getTransform(), setTransform() functions.
Example
The following example shows how important the matrix hierarchy.
In this example, we create get the node from the editor and clone it. Then we change the transformation matrices of these node: we examine two cases
- when there are two independent nodes
- when one node is the child of another
In the AppWorldLogic.h file, define the material_ball child and parent nodes smart pointers.
// AppWorldLogic.h
/* ... */
class AppWorldLogic : public Unigine::WorldLogic {
public:
/* .. */
private:
Unigine::NodePtr material_ball_child;
Unigine::NodePtr material_ball_parent;
};In the AppWorldLogic.cpp implement the following code:
// AppWorldLogic.cpp
#include "AppWorldLogic.h"
#include "UnigineEditor.h"
#include "UnigineVisualizer.h"
#include "UnigineConsole.h"
#include "UnigineLog.h"
using namespace Unigine;
using namespace Unigine::Math;
int AppWorldLogic::init() {
// enable the visualizer for world origin rendering
Console::get()->run("show_visualizer 1");
// get the material ball from editor and clone it
material_ball_child = Editor::get()->getNodeByName("material_ball");
material_ball_parent = material_ball_child->clone();
// make the one node the child of another
material_ball_parent->addChild(material_ball_child);
// create rotation and translation matrices for the first material_ball
Mat4 rotation_matrix = (Mat4)rotateZ(-90.0f);
Mat4 translation_matrix = (Mat4)translate(vec3(3.0f, 0.0f, 0.0f));
// create translation matrix for the second (parent) material ball
Mat4 translation_matrix_clone = (Mat4)translate(vec3(0.5f, 0.0f, 1.0f));
// create new transformation matrices for the material balls
Mat4 transform = material_ball_child->getTransform() * translation_matrix * rotation_matrix;
Mat4 transform_clone = material_ball_parent->getTransform() * translation_matrix_clone;
// set the transformation matrices to the material balls
material_ball_child->setTransform(transform);
material_ball_parent->setTransform(transform_clone);
return 1;
}
int AppWorldLogic::update() {
// render world origin
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(1.0f,0.0f,0.1f), vec4(1.0f,0.0f,0.0f,1.0f));
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(0.0f,1.0f,0.1f), vec4(0.0f,1.0f,0.0f,1.0f));
Visualizer::get()->renderVector(Vec3(0.0f,0.0f,0.1f), Vec3(0.0f,0.0f,1.1f), vec4(0.0f,0.0f,1.0f,1.0f));
return 1;
}
int AppWorldLogic::shutdown() {
// clear smart pointers
material_ball_child.clear();
material_ball_parent.clear();
return 1;
}If you comment the following line
// make the one node the child of another
material_ball_parent->addChild(material_ball_child);you'll get another result:

|

|
|
Parent-child nodes
|
Nodes are independent
|
When nodes are independent they have different local and world transformation matrices. In case of parent-child nodes, the child's local transformation matrix after moving remains the same, but the world transformation matrix will be changed (you can check it by using debug profiler).