Scene Geometry

In a virtual world, a three-dimensional object is typically represented as a collection of points with coordinates, edges connecting these points, and faces stretching across these edges. Let's go through all these components.
A point, also known as a vertex, is the foundation. Without points there will be nothing, neither a cube, nor even a line. Points, however, can exist on their own and have their own coordinates.
An edge is a connection of two points, or a segment in three-dimensional space. It is defined by the points it connects and the line itself.
Percieving only points and edges is not an easy task, therefore, edges form a frame across which faces are stretched, which allow us to see the object painted in any color or using materials that determine its appearance.
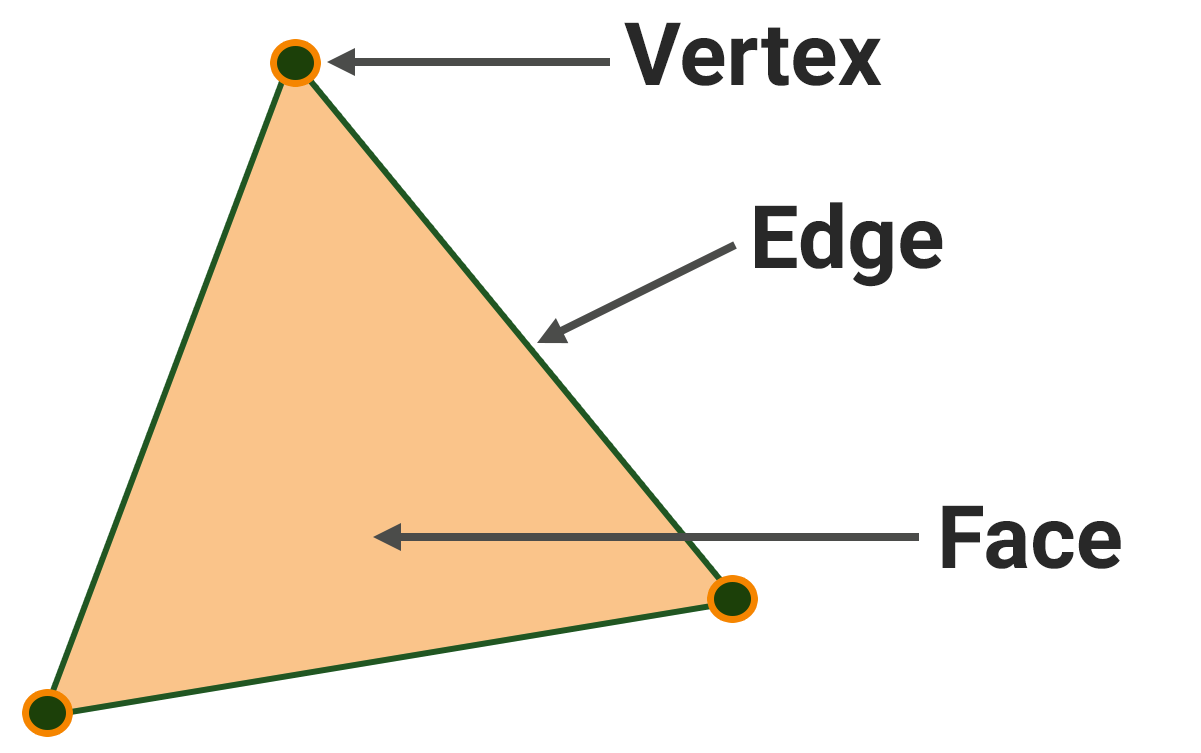
So, a face is stretched across a closed contour of edges (i.e. its starting point coincides with the end point). The minimum number of face edges is three, if it's less, then we'll have an edge. An important notice here: a face with 3 edges cannot be bent — no matter which vertex we pull, all its edges will always lie in one plane. This is crucial for computer calculations, so a face stretched across a closed contour of 3 edges — a triangle — is an important element of geometry, along with a point and an edge. A triangle is characterized by the coordinates of its vertices, the edges, and the normal.
The normal is a computer characteristic needed to calculate lighting. A triangle has two surfaces - an outer surface facing outward from the object and an inner surface facing inward. Light falls on the surface of the triangle from the outer side, and the normal vector is the vector going outwards from the triangle at the right angle to its surface. The inner sides of faces are often not drawn, and if you look at a face from inside the object, it won't be visible.
All faces having more than three edges, and any surface in general, can be approximated with triangles to a sufficient degree of accuracy. The word sufficient in this case refers to the minimum number of triangles required to achieve an acceptable appearance of the surface, as adding more triangles can increase the load on the renderer (while reducing it is one of the crucial tasks). This process of dividing a surface into triangles is known as triangulation, while increasing the level of detail on an already triangulated surface is called tessellation. Graphics APIs such as Vulkan and DirectX, as well as graphics cards, exclusively operate with triangles.
Of course, while creating a model, no one manually breaks all its faces into triangles — there are algorithms available specifically for this purpose. Thus you can create faces as polygons, which are sets of triangles lying in one plane and touching each other with edges.

Closed frame of edges
|
Frame triangulation
|

Polygon in the frame
|
By connecting edges (polygons or triangles) lying in different planes, we get what is called an object.
So, the fundamental geometric concepts in 3D are point, edge, triangle (the elementary ones), and polygon (the derivative one). And an object is just a container for geometric elements.
Mesh and Its Surfaces#
A mesh is a set of vertices, edges, and triangular faces (organized into polygons) that define the geometry of an object. Meshes include one or more groups of polygons, which are called surfaces.
A surface is a subset of the object geometry (i.e. a mesh) that does not overlap other subsets. Each surface can be assigned its own material or property. In addition, surfaces within a mesh can be organized into a hierarchy, and each surface can be switched on or off independently of the others — this can also be used for switching between levels of detail (LOD), we'll discuss this later. Thus, a surface can represent:
- Part of the object to which an individual material is assigned (for example, a magnifying glass may have two surfaces — a metal ring with a handle and the glass itself).
- One of the levels of detail (LOD), including LODs for reflections and shadows. In this case, the surfaces represent the same object or its part in a more or less detailed form (high- and low-polygonal meshes). Each surface has a set of properties that allow defining the visibility distance (the farther away from the camera, the less detailed surface is required to be rendered).
This is why one mesh can have many surfaces. The quadcopter mesh in the picture below consists of four sufraces: moving part of the frame (arms and protection), body, small parts, and landing gear and propellers.

The most commonly used object is Static Mesh — it can be moved, rotated and scaled, but the geometry itself cannot be changed: the positions of their vertices are unchanged.
Object models are created in third-party graphics programs (such as 3ds Max, Maya, etc.) and can be imported through UnigineEditor — their geometry is converted into UNIGINE's own format (*.mesh). In UNIGINE, meshes have 32-bit precision, so we recommend placing meshes at the origin before exporting them from third-party graphics programs, and then placing the mesh in UnigineEditor.
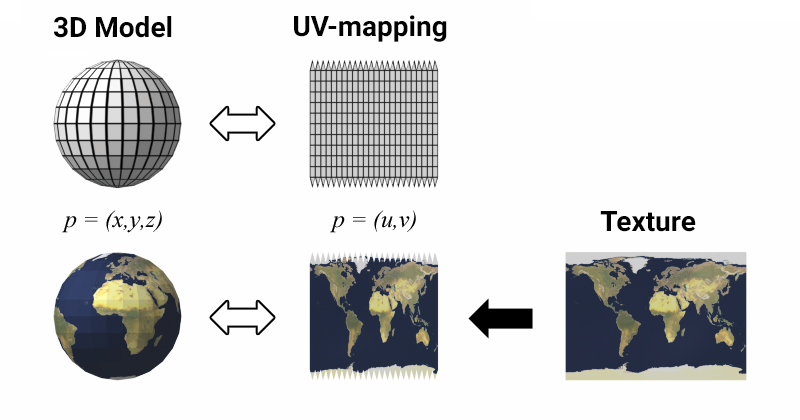
In 3D modeling, surfaces are rendered as individual elements that require their own DIP rendering call. To render a surface, a material must be assigned to determine its appearance, such as whether it will be matte or glossy and have a wood or brick texture. Textures are used to set the color and texture of the surface at each point and are overlaid onto the model's surface using a UV map or map stored within the model (we'll review materials and textures in more detail later). This map converts (X,Y,Z) space coordinates to UV space coordinates, with U and V coordinates taking values from 0 to 1. Modern video cards consider the UV transformation within a single triangle to be affine, requiring only U and V coordinates for each vertex. So, it is up to 3D modelers to decide how to connect the triangles to each other, and creating a successful unwrapping is an indicator of their skill level.
There are several mapping quality parameters, which may be contradictory:
- Maximizing the use of texture space. Compact layout is necessary for efficient memory use and higher texture detail on the model. However, keep in mind that a certain allowance is required at the edges of the unwrapping to generate smaller textures.
- Avoiding areas with excessive or insufficient detail.
- Avoiding areas with excessive geometry distortions.
- Maintaining the viewing angles from which an object is usually drawn or photographed to simplify the texture artist's work.
- Effectively locating seams — the lines that correspond one edge but are positioned in different areas of the texture. Seams are desirable if a surface has a natural interruption (clothing seams, edges, joints, etc.) and should be avoided if there is none.
- For partially symmetrical objects: combining of symmetrical and asymmetrical parts of the layout. Symmetry increases texture detail and simplifies the artist's work; asymmetrical details juice up the object.
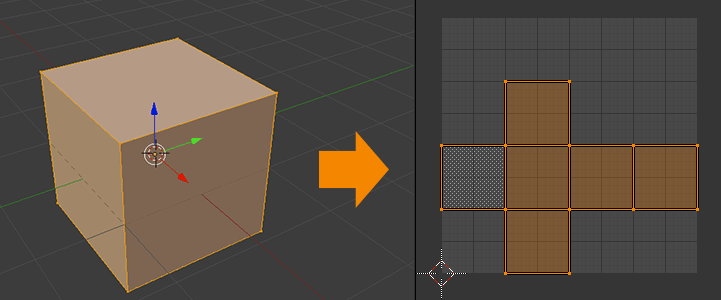
The unwrapping can be done either manually or automatically, and many tools (Maya, Blender, 3D Max, and others) offer an auto unwrapping feature. UNIGINE has this functionality too, and you can generate a UV unwrapping at the model import, which can be used for lighting maps or for drawing directly on the object.
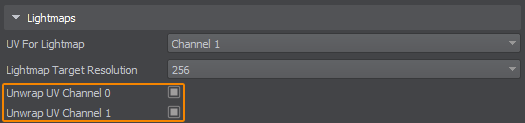
Each surface in UNIGINE has 2 UV channels. You can specify in the material settings which UV channel to use. For example: the first UV channel can be used for tiling and detail textures, and the second for light maps.
The information on this page is valid for UNIGINE 2.19.1 SDK.